这堂橄榄树小学四年级数学课上，每个同学们都拿出了一块“头脑风暴讨论板”。只见他们拿着笔，在白板上郑重其事地想象着：“假如我要去露营旅行，我会带哪些物品？”

 

 

-山上会不会有蛇啊？
-有！我要带一瓶雄黄酒。
– 我要带一把刀防身。

 

-食物一定要带啊！
-我可以吃山上的野果子。

 

-我准备了睡袋，因为山上昼夜温差很大。
-手表可以用来测试我的心率。

 

-你怎么还要带作业去露营啊！
-我想带信号弹，可以和外界保持联系。

 

在小朋友们可可爱爱的头脑风暴中，
开始了今天的橄榄树数学思维课程。

 

 

 

 

01 贴近学生生活的情境

 

 

在课程开始前，曹老师就做了一个小调查：“有多少同学有露营的经历呀？”没想到同学们都很兴奋，不仅有人爬过南太行，还有人告诉曹老师自己每周都去露营。于是，曹老师创造了一个贴近同学们生活的真实有趣的情境——露营旅行。通过头脑风暴讨论板上的内容，我们可以看到，同学们对露营既有规划和憧憬，又天马行空。同样也热爱露营的曹老师告诉同学，露营背包通常以“升”（L）为单位来表示。10-20升一般适用于短途徒步或日间露营，20-40升则适用于多日徒步或轻量级露营等。

 

 

 

 

规划完了自己的露营清单后，曹老师问道：“假如我们背包中还可以再装3L的物品，如何选择可以获得更高的使用价值呢？” 同学们可以在望远镜、急救包、露营帐篷中进行选择，而这三样物品也分别有不同的使用价值和重量。按照最常规的列举法，同学们写出了8种组合方式，再判断重量，发现其中只有4种组合方式可以放入3L的背包中，然后再选出使用价值最高的方案。但当物品增加到四种、五种、N种呢？同学们发现，如果一个个列出来，再判断最优组合方式，会变得越来越复杂并且难以计算。

 

 

02“奥利凡德的魔杖”

 

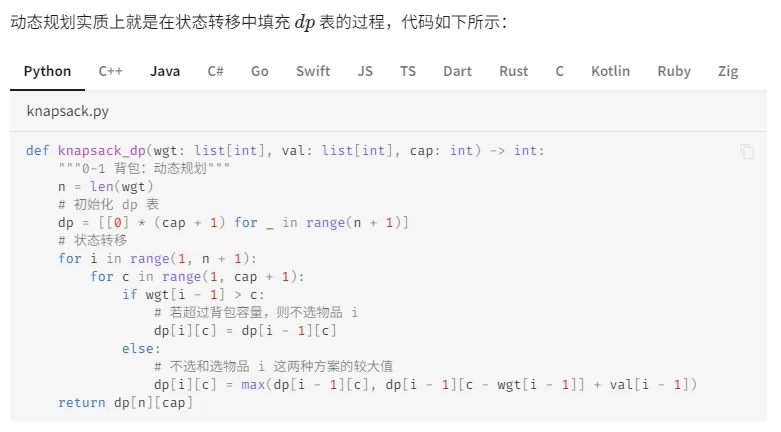
同学们遇到的其实就是算法中经典的「背包问题（Knapsack Problem）」。他们需要运用「动态规划（Dynamic Programming）」，也就是把原问题分解为相对简单的子问题，来解决不断变化的条件限制下的复杂问题。如果用代码则如下所示：

 

 

不过，这是一堂小学四年级的数学思维课。程序员使用这套算法可以解决许多运营等优化需求，而小学生要了解的就是其背后的数学逻辑支撑。在这样的数学思维课里，老师们都会创造一个与学生生活相关的情境，然后使用我们称之为“魔杖”的神奇教具。同学们收到了一份任务卡，分别列有1L、2L和3L的背包，可以通过贴纸的方式来放置物品，且物品也会逐步增加。

 

 

其背后的原理就是动态规划，即将3L的背包（原问题），拆分为1L和2L（相对简单的子问题），通过在表格中排列对比，同学们很快可以发现规律：当我们逐个添加物品时，都是先解决小背包问题，再利用已知的结果，考虑大背包问题。即便再添加一件更小的0.5L的物品，同学们也可以继续拆分背包，找到最优解。

 

 

03当我们谈论“未来”时 我们在谈论什么？

 

此时，孩子们再次拿出那块头脑风暴讨论板，开始真正思考：“如果我有15L的背包，究竟可以装下哪些东西，并且还要具有最高使用价值？”他们没有急于下结论，而是根据自己的量感，估算每一件物品的体积，并标注了自己心目中认为的使用价值。最后再圈圈划划，列出了最优的方案。之前我们考虑把雄黄酒、防身小刀、信号弹、平板、作业……能带的都带上。现在我知道了，要考虑容量和使用价值。不是越多越好，而是选择价值最高的东西。

 

 

为什么橄榄树小学要学如此抽象的动态规划？事实上，我们这门有趣好玩的数学思维课，是为了培养同学们的计算思维。计算思维不等于编程，更不等于计算机思维。计算思维并不是为了帮助同学们做题、考试，更不是让孩子们像计算机一样做事。而是能够将复杂问题进行抽象、分解、建模，并设计算法，形成解决方案，并学会迁移。就像背包问题，其核心在于权衡与取舍，同学们会发现小到学习计划制定、小组分工合作，大到医疗资源分配、投资组合优化、药品物流运输等，都会用到动态规划背后的底层逻辑。

 

 

 

--- END ---